本記事では,アレニウス式の導出・使い方について解説しています.
アレニウス式の導出
化学反応には,基本的に温度依存性(一般には温度が高いほど反応は促進される)があることが知られています.そこで,当該化学反応における速度定数を\(k_r\),\(k_r\)を測定した際の実験温度を\(T\)として,縦軸に ln\(k_r\),横軸に\(1/T\)をとり,プロットすると右肩下がりの直線式を得ることができます.
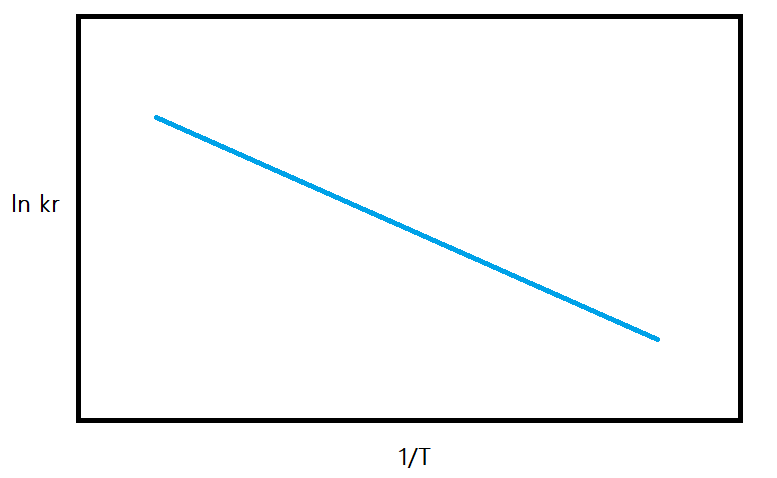
アレニウスプロットは直線状ですから,中学校数学で習う一次関数の式(\(y=ax+b\))のように,表すことが出来ます.
まず,上のグラフをそのまま式にすると,次のようになります.
$$ \text{ln}k_r = \text{傾き} \times \frac{1}{T}+ \text{切片} $$
ここで,傾きと切片を次のパラメータで表します.
\(A\):頻度因子(切片に対応する.)単位は,\(k_r\)と同じになります.
\(k_r\)の単位は,\(\text{dm}^3 \text{mol}^{-1} \text{s}^{-1} \)(一例)です.
\(E_a\):活性化エネルギー(傾きに対応する.)単位は,\(\text{kJ mol}^{-1}\)です.
傾きは\(-\frac{E_a}{R}\),切片は\(\text{ln}A\)でそれぞれ表すことができます.
以上をまとめると,先ほどの一次関数式は次のように表すことができます.
$$ \text{ln}k_r = -\frac{E_a}{R} \times \frac{1}{T}+ \text{ln}A $$
$$ \text{ln}k_r = \text{ln}A -\frac{E_a}{RT} $$
自然対数を外した次の形で表すこともあります.
$$ k_r = Ae^{-\frac{E_a}{RT}} $$
演習問題1
問:アレニウスプロットにおいて,活性化エネルギー(\(E_a\))が低下すると,反応はどのようになるか? また,この活性化エネルギーの低下を誘発する物質は何か?
答:速度定数の温度依存性は小さくなる.活性化エネルギーが低い経路は,触媒がつくる.
アレニウス式の使い方
演習問題2
問:ある化学反応について,その活性化エネルギーを求めたい.活性化エネルギーを求めるには,どうしたらよいか,方法を論じなさい.
答:まず,温度(\(T\))と速度定数(\(k_r\))のデータを実験により収集する.
次に,横軸に温度の逆数(\(1/T\)),縦軸にln(\(k_r\))をとり,上記の実験データをプロット
する(アレニウスプロット).
続いて,最小二乗法等を適用し近似式(一次直線式)を得た後,\(E_a = -R \times \text{傾き}\)
により,活性化エネルギーが求まる.
補足:\(e^{切片}\)により,頻度因子を求めることができます.
切片(ln\(A\))は,実験誤差の影響を受けやすいパラメータです.また,切片付近の領域は必ず
しも直線とは限りません.従って,(ln\(A\))の信頼度については注意が必要です.
アレニウス式の利点
アレニウス式の良さは何と言っても,化学反応の温度依存性を簡単に(一次式)で記述可能な点です.特に,生体活動や生体内の化学反応は,温度と密接な関係があることが知られています.これを,一次式という最もシンプルな形で表現できるのは魅力的ですね.

コメント